In 2024, Bitcoin remained the driver of the cryptocurrency market, which set the direction and growth rates for other coins. From January to December, the main digital asset increased in value by more than 60% (from $29.08 thousand to $47.87 thousand). At the peak, the currency rate reached $69 thousand. Over the year, BTC capitalization increased 1.7 times (from $543.88 billion to $924.61 billion). The reason for such popularity is a combination of factors: security, anonymity, lack of borders and others. But the main one is Bitcoin’s math, on which the cryptocurrency is built. Thanks to the synergy of elliptic curves and finite fields, the system works well.
The basis of Bitcoin’s math
Cryptocurrency completely changes the usual definition of ownership. In the traditional world, to own something means to dispose of its physical expression. Blockchain works differently. Digital coins are records in a distributed ledger that have no physical equivalent. To own bitcoin implies disposing of it at will by recording transactions on the blockchain.
A record of ownership becomes a much more secure way to keep possessions than a traditional safe deposit box or safe deposit box.
This ability is provided by the Elliptic Curve Digital Signature Algorithm mechanism. It is a cryptographic signature system built on elliptic curves and finite fields. It cannot be forged and its validity can be easily verified by anyone in the network.
ECDSA includes 2 separate procedures for signature creation and verification. Each is a mechanism that combines several mathematical operations. The first uses a private key to activate the transaction. The second verifies it through a public character set.
5020 $
bonus for new users!
ByBit provides convenient and safe conditions for cryptocurrency trading, offers low commissions, high level of liquidity and modern tools for market analysis. It supports spot and leveraged trading, and helps beginners and professional traders with an intuitive interface and tutorials.
Earn a 100 $ bonus
for new users!
The largest crypto exchange where you can quickly and safely start your journey in the world of cryptocurrencies. The platform offers hundreds of popular assets, low commissions and advanced tools for trading and investing. Easy registration, high speed of transactions and reliable protection of funds make Binance a great choice for traders of any level!
Elliptic Curves
The concept of ECDSA was introduced in 1992 by cryptographer Scott Vanstone. In it, an elliptic curve is shown by marks on a graph, the order of which can be described by the formula: y2 = x3 + ax + b. In the BTC protocol, a is taken as 0 and b is equal to 7. Graphically, this element looks like this:
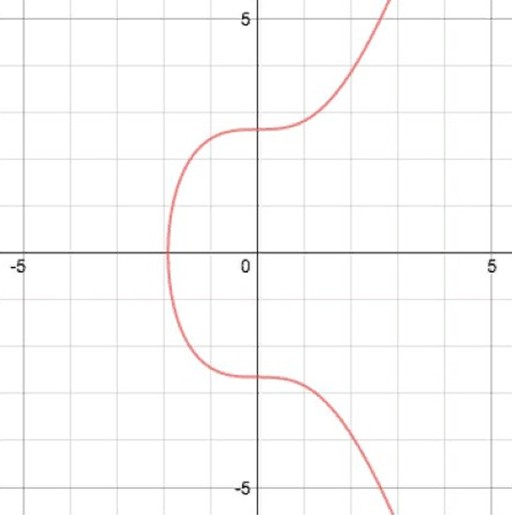
The element has several useful features:
- A non-vertical line passing through the curve at 2 points will necessarily intersect it at 3 points as well.
- If such a line touches the elliptic element in one place, it will pass through it in another.
These characteristics are used in the addition and doubling of points. In the first case, a straight line must be drawn through the summands P and Q (on the graph). It will intersect the curve at the point R′. After this it is necessary to find on the elliptic line a mark opposite in value to R′. It can be called R and taken as the sum of P and Q.
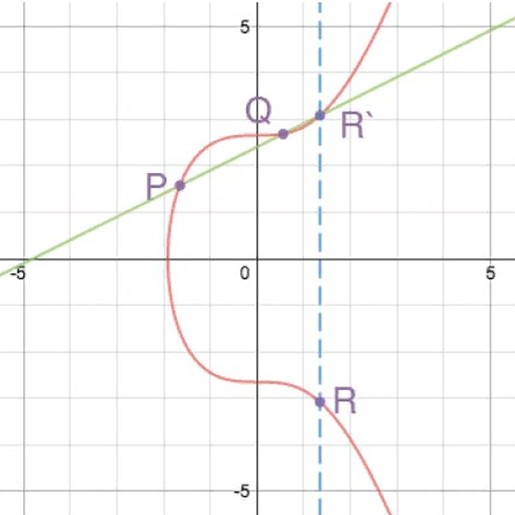
To double the value, the formula P + P = R is used. A line is drawn on the graph that touches the curve at the mark P. Considering the characteristics of the element, the segment should intersect it at the point R′, the opposite of R. In this case, R is taken as the doubling mark.
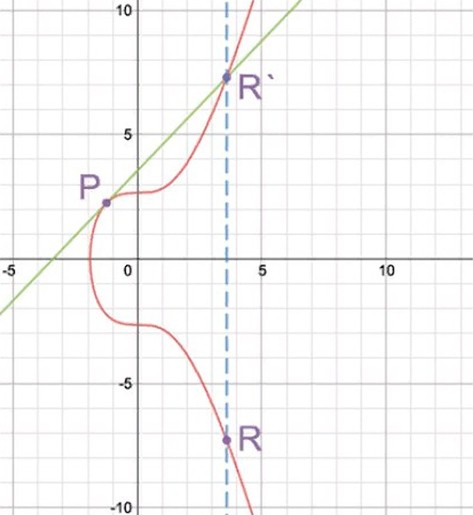
These 2 calculations are needed to determine the scalar product R = aP (adding the mark P to itself a number of times).
For BTC, R = 7P or R = P + (P + (P + (P + (P + (P + (P + P))))).
If you simplify, you get:
R = P + 6P
R = P + 2 (3P)
R = P + 2 (P + 2P).
Thus, the operation is divided into 2 steps on doubling the mark and 2 on addition. For working with complex numbers, faster methods are used.
Finite fields
In cryptography, the same curve is used, but considered in certain numerical limits. This is a finite field into which the results of all calculations theoretically fall.
Sometimes the values obtained go beyond certain limits. In this case, it is necessary to end the operation, and then return to the beginning of the range and continue the calculation. In this way, the result will always be inside the final field.
As an example, we can determine the remainder of division by an integer (modulus operation – MOD): 9/7 = 1 with a remainder of 2. The operation has the value: 9 MOD 7 = 2. The boundaries of the finite field are 0 and 6. This means that the results of all modulus 7 calculations, regardless of the original number, will fall within the specified range.
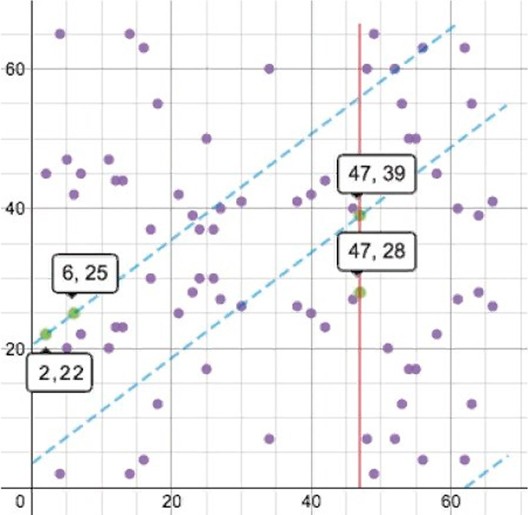
The elliptic curve of Bitcoin using the formula y2 + x3 +7 is defined on the finite field modulo 67. On the graph, this is expressed by a cluster of marks. All x and y values in them are integers in the range 0-66. Straight lines wrap around the selected space once they reach the number 67, to continue on the other side. If you add up the marks 2, 22 and 6, 25, the line passing through them will intersect the third, 47, 39. The result of the calculation will be the opposite mark 47, 28.
Use in cryptography
The bitcoin protocol fixes values for an elliptic curve and a given space. Therefore, each member of the network can only apply certain formulas. The fixed characteristics include:
- Elliptic element formula (equation).
- Basepoint.
- Primemodulus.
- The orderof the base point (order).
Bitcoin math uses complex numbers for these values. They ensure the security of the cryptocurrency network, because it is almost impossible to find a private key to a transaction or wallet by a simple brute force method. The calculation of values for BTC is presented in the table.
| Indicator | Result |
|---|---|
| Elliptic element formula | y2 = x3 + 7 |
| Finite field modulus | 2²⁵⁶ – 2³² – 2⁹ – 2⁸ – 2⁷ – 2⁶ – 2⁴ – 1 = FFFFFFFFFF FFFFFFFFFF FFFFFFFFFF FFFFFFFFFF FFFFFFFFFF FFFFFFFFFF FFFFFFFFFF FFFFFFFFFFFF FFFFFFFFFF FFFFFFFFFFFF FFFFFFFFFFFFFF FFFFFFFFFFFF FFFFFFFFFFFF FFFFFFFFFFFFFF FFFFFFFFFFFFFFFF |
| Base point | 04 79BE776E F9DCBBDC 54A06275 CE870B27 023BFCDB 2DCE58D9 59F2817B 26F81778 443ADA77 26A3C875 5DA5TBFC 0E2208A8 FH15B448 A6854419 8C48D08C FB10D5B8 |
| Order | FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE4 AF47A04B BFD25E8C D0366141 |
This sequence of values is called secp256k1. In the Bitcoin protocol, it is used in conjunction with the ECDSA scheme. The system sets the private key to a number between 1 and an order of magnitude. The public one is obtained from the secret one by the method of squared multiplication by the base mark index.
If too complicated
The bitcoin blockchain is built on mathematical principles. The network uses a digital signature scheme, ECDSA, to send transactions. The mechanism works based on elliptic curves calculated within certain numerical limits. With the help of these functions, a complex system of generating private and public addresses is created.
On the one hand, the mathematical order of creating a digital signature shows that the maximum number of bitcoin wallets is defined. But on the other hand, the complexity of the calculations increases exponentially. It would take about 2¹²⁸ attempts to solve the problem. This would take an amount of time comparable to the existence of the universe.
Frequently Asked Questions
❓ What is ECDSA?
The cryptographic mechanism for digital signatures is the system on which the Bitcoin blockchain is based. They cannot be forged and authenticity is easily verified by anyone on the network.
🔑 Why do the Bitcoin blockchain have private and public keys?
The first one activates a transaction. The second allows you to verify it with a simple combination of characters.
📈 What is an elliptic curve?
The algebraic term refers to the set of points on a graph that correspond to a certain equation. In cryptography, these elements are used as a tool to build a blockchain.
✅ Why is bitcoin impossible to counterfeit?
The network is built on mathematical operations that use huge numbers to create private and public addresses. It is impossible to decipher the secret codes.
❕ What are finite fields?
Calculations in the blockchain are made within certain values. This is the field where the results of all calculations are recorded.
A mistake in the text? Highlight it with your mouse and press Ctrl + Enter.
Author: Saifedean Ammous, an expert in cryptocurrency economics.
English (United States) 
English (UK) 
Arabic 
Bulgarian 
Hungarian 
Greek 
Danish 
Indonesian 
Spanish 
Italian 
Chinese 
Korean 
Latvian 
Lithuanian 
German 
Dutch 
Norwegian 
Polish 
Portuguese (Portugal) 
Portuguese (Brazil) 
Romanian 
Slovak 
Slovenian 
Turkish 
Ukrainian 
Finnish 
French 
Czech 
Swedish 
Estonian 
Japanese